Probleemoplossen, hoe doen ze dat?

Bij het oplossen van een natuurkundeopgave blijven leerlingen vaak hangen in een bepaalde aanpak. Deze houden ze minutenlang vol zonder dat dit iets oplevert.

[collapsibles]

Hoe lossen ze dat op?

Het oplosgedrag waarbij de leerling, een beginner, in een bepaalde aanpak blijft hangen, is geobserveerd door Tuminaro & Redish (2007). Zij karakteriseren dit oplosgedrag met zes types aanpak, zogenaamde “epistemic games”. Deze typering kan helpen bij het herkennen en desgewenst bijsturen van leerlinggedrag.

Zes manieren om een probleem te lijf te gaan

Van betekenis naar formule – In deze aanpak komen de volgende stappen voor: (1) Probeer te begrijpen wat er aan de hand is. (2) Identificeer de gevraagde grootheden. (3) Relateer de grootheden aan het verhaal uit de eerste stap. (4) Voer de benodigde berekeningen uit. (5) Controleer je antwoord, bv met een antwoordenboek.

Van formule naar betekenis – Hier gaat het net andersom. De formule komt snel op tafel, daarna kijken we hoe ver we komen. De volgende stappen worden onderkend: (1) Identificeer de belangrijkste concepten. (2) Zoek een formule waarin deze concepten samen komen. (3) Probeer nu te begrijpen hoe deze formule kan beschrijven wat er aan de hand is. (4) Check je antwoord.

Kwalitatief beschrijvend – In deze aanpak wordt (1) geredeneerd vanuit de fysieke situatie, waarna (2) meteen een conclusie wordt getrokken, vaak zonder daarbij fysische concepten of formules te gebruiken. Het besef dat de opgave nog niet is afgerond ontbreekt. Wordt wel verder gegaan, dan komt de ‘van betekenis naar formule’ aanpak in beeld.

Grafische analyse – Zodra duidelijk is (1) waar we naar op zoek moeten, wordt (2) een figuur getekend. Dat kan een circuit met weerstanden zijn of een voorwerp waarop krachten worden getekend. (3) Aan de hand van de figuur wordt het probleem geanalyseerd en (4) worden ontbrekende grootheden, vectoren of waardes verkregen.

Recursief vergelijkingen invullen – Het eigenlijk alleen in formules denken. (1) Ga na wat er wordt gevraagd. (2) Zoek een geschikte formule. (3) Vul deze zoveel mogelijk in en check of een oplossing mogelijk is? Zo nee, zoek er een geschikte formule bij. Zo ja, invullen en klaar. Vindt er toch reflectie plaats op wat je eigenlijk hebt gedaan, dan komt ‘van formule naar betekenis’ weer in beeld.

Hergebruik van een uitwerking – De stappen zijn: (1) Ga na wat er wordt gevraagd. (2) Zoek een uitgewerkte opgave die hier bij lijkt te passen. (3) Vul de waarden van het nieuwe probleem in. (4) Ga na of je een oplossing hebt gevonden.

Voorbeeld: Het probleem met de 3 ladingen

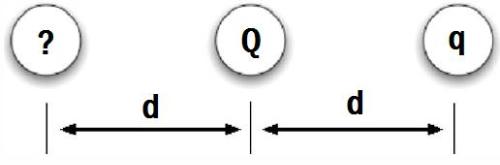
Het drie-ladingenprobleem.

In de figuur met de 3 ladingen is het de vraag hoe de linker en de middelste lading zich verhouden als gegeven is dat de rechter lading niet van positie verandert? Volgens Tuminaro en Redish zijn experts hier binnen een minuut uit. Coulomb, elkaar opheffende krachten, superpositie, experts combineren deze zaken moeiteloos. Hun eigen studenten blijken hier, werkend in groepjes, zo 45 minuten mee bezig te zijn! Daarbij vastlopend in een bepaalde aanpak, of ‘switchend’ van de ene aanpak naar de andere. Zo blijken studenten in de war te raken omdat er een lading tussen zit. Zou deze middelste lading de werking van de buitenste lading niet blokkeren? Allerlei niet-fysische principes worden verkend en gebruikt.

Discussie

Eens te meer wordt duidelijk hoe verschillend beginners en experts problemen aanpakken. Deze studie gaat net een niveau dieper waardoor die verschillen beter benoemd kunnen worden. Aan de docent de schone taak hier en daar een hint te geven zodat leerlingen besluiten een alternatieve, meer solide aanpak ter hand nemen.

Referentie

• Tuminaro, J. & Redish E.F. (2007). Elements of a cognitive model of physics problem solving: Epistemic games. Physical Review Special Topics – Physics Education Research 3, 020101. The American Physical Society.

[/collapsibles]